Singular Values-Driven Automated Filter Pruning

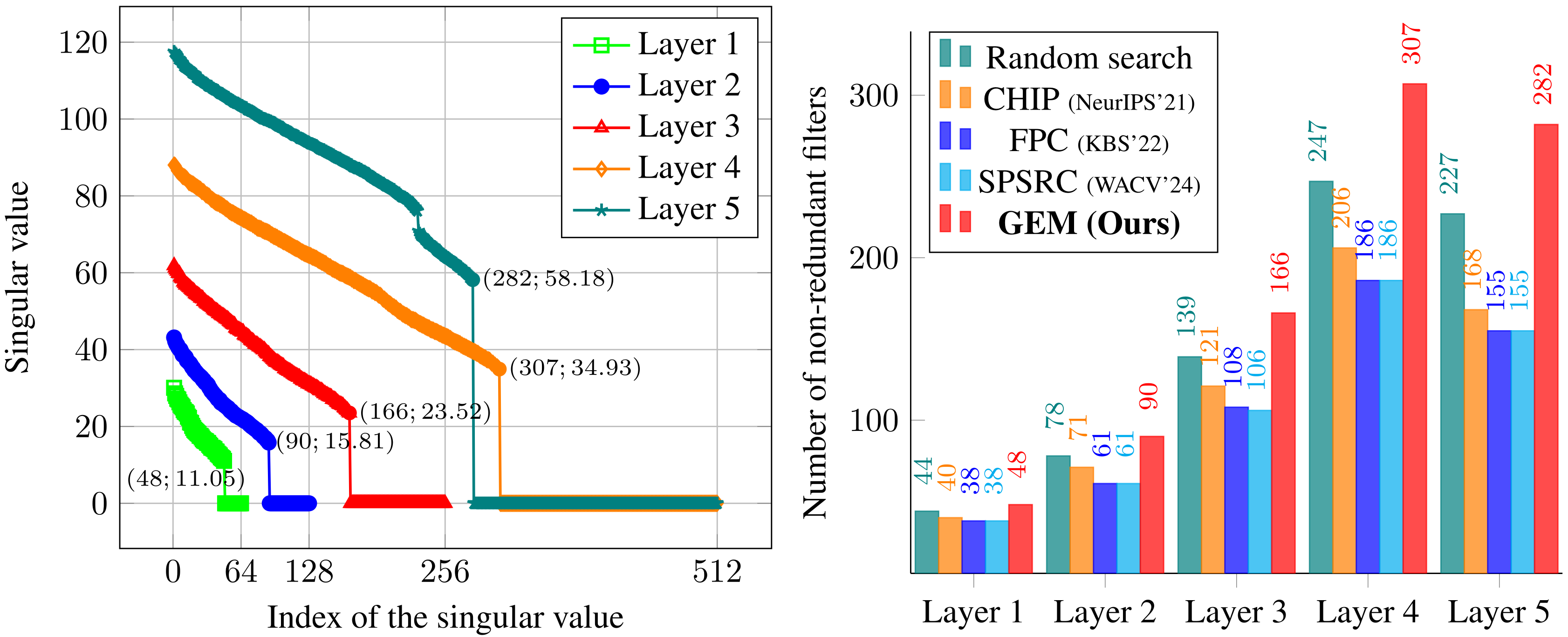
This paper proposes a method that leverages tools from linear and multilinear algebra to provide a new solution for automated filter pruning. We propose to detect network redundancy hinging on the dynamics of singular values and the use of the nuclear norm. We illuminate the intricate relationship between filter redundancy within neural networks and the observable variations in their singular values. To illustrate the rationale of our proposed approaches, we create a synthetic dataset, dubbed as SVGG, which includes an original model that mimics the architecture of the VGG network with \(L=5\), \(d_l= 3\) and \(\{C_l\}_{l=1}^L = \{64, 128, 256, 512, 512\}\). We choose the redundant rates (the ratio of the number of redundant filters to the total number of filters, i.e., \(\frac{C_l-N_l}{C_l}\)) of these layers sequentially as \(\{0.25, 0.3, 0.35, 0.4, 0.45\}\), thus \(\{N_l\}_{l=1}^L = \{48, 90, 166, 307, 282\}\), and the number of retained filters \(N=893\). In the \(l\)-th layer, we init \(N_l\) core filters with the standard normal distribution while the remaining redundant filters are copied from the core filters with a small noise of variance \(\epsilon = 0.01\). The "multilinear" singular values are visualized as follows. One should note that the overparameterized model contains many near-zero singular values, indicating redundancy. The random search approach, CHIP, FPC, and SPSRC yield suboptimal results, whereas GEM successfully identifies all unique filters, achieving 100% accuracy comparable to the complete search, with reduced computational overhead.

To showcase SLIMING's adaptability, we evaluate it on five architectures: VGG-16-BN, GoogLeNet with inception modules, ResNet-20/32/56/110 with residual blocks, DenseNet-40 with dense blocks, and MobileNetV2 with inverted residual blocks. These models are tested on the CIFAR-10/100 datasets. To further validate SLIMING's scalability, we perform experiments on the ImageNet dataset using ResNet-50 and MobileNetV2 architectures. Additionally, the compressed ResNet-50 model is used as the backbone for Faster R-CNN-FPN, Mask R-CNN, and Keypoint R-CNN on the COCO-2017 dataset. We compare SLIMING with 56 related works, as detailed in the paper, and present ResNet-50 results on ImageNet in Table 1 for clarity. Our method consistently surpasses other approaches across all compression levels in terms of performance and complexity reduction.

To emphasize the practical benefits of SLIMMING, we meticulously conducted an experiment comparing a baseline model with a compressed model, both designed for object detection tasks. Using the FasterRCNN_ResNet50_FPN architecture on an RTX 3060 GPU, the experiment robustly demonstrates the significant performance improvement achieved by SLIMMING. Accompanying GIFs provide a clear visual representation: the baseline model achieves an inference speed of approximately 9 FPS, while the SLIMMING-compressed model achieves a remarkable twofold increase in throughput. This substantial difference effectively demonstrates SLIMMING's effectiveness and scalability, firmly establishing its relevance and usefulness across various deployment scenarios.

We present a qualitative evaluation of feature preservation, complementing the established efficiency demonstrated through numerical results. Our analysis involves a random selection of 5 images from the ImageNet validation dataset, examining three compression levels applied to the original ResNet-50 model: 44%, 63%, and 79%. Utilizing GradCAM for interpretation, we visually assess and analyze feature maps in both the original and compressed models. The visual representation underscores our framework's efficacy in retaining crucial features across a diverse range of classes. Noteworthy is its consistent robustness in capturing and preserving essential information at different CRs. This resilience implies sustained effectiveness and reliability across varying scenarios and compression levels, positioning our framework as a versatile choice for network compression across diverse applications and datasets.

The ever-accelerating progress of technology… gives the appearance of approaching some essential singularity. — John von Neumann, 1958

The singularity is nearer. — Ray Kurzweil, 2024